A New Method for Enhancing Neural Network Training

American Express is known for having best-in-class credit ratings and fraud detection. More than 800 American Express colleagues work together to provide precise data that drives informed credit decision. One of the ways we stay at the forefront of data science research, discover cutting-edge technologies, and connect with emerging talent is through partnerships with colleges and universities across the globe. We have a long-standing relationship with Imperial College London’s Department of Mathematics. Every year, we supervise graduate students on their Summer Research Project and focus on identifying promising technical challenges that can meaningfully impact our work in risk assessment and fraud detection.

Our latest collaboration led to the development of EDAIN (Extended Deep Adaptive Input Normalization), a novel preprocessing technique that improves how neural networks handle complex financial time series data. Based on our results, we were able to publish the paper at the AISTATS conference a few years ago. We’ll dive into the challenge we tackled, the solution, the results we’ve seen so far with the EDAIN technique, and the future steps for research.

Preprocessing Complex Financial Data

In credit risk and fraud detection, our data presents unique challenges:

• Transaction patterns often show multiple distinct behaviors, which can cause the data to be distributed with multiple modes (see D_48 as an example in Figure 1);
• Credit utilization tends to be unevenly distributed, causing feature values to be distributed according to a power law, which causes skewness in the data. This is illustrated with the D_39 feature shown in Figure 1;
• Unusual spending behavior creates outliers (see for example P_2, Figure 1);
• Many customer characteristics used in modelling have a high proportion of missing values;
• Due to changing macroeconomic conditions, customer characteristics also change over time, making the time series features non-stationary.

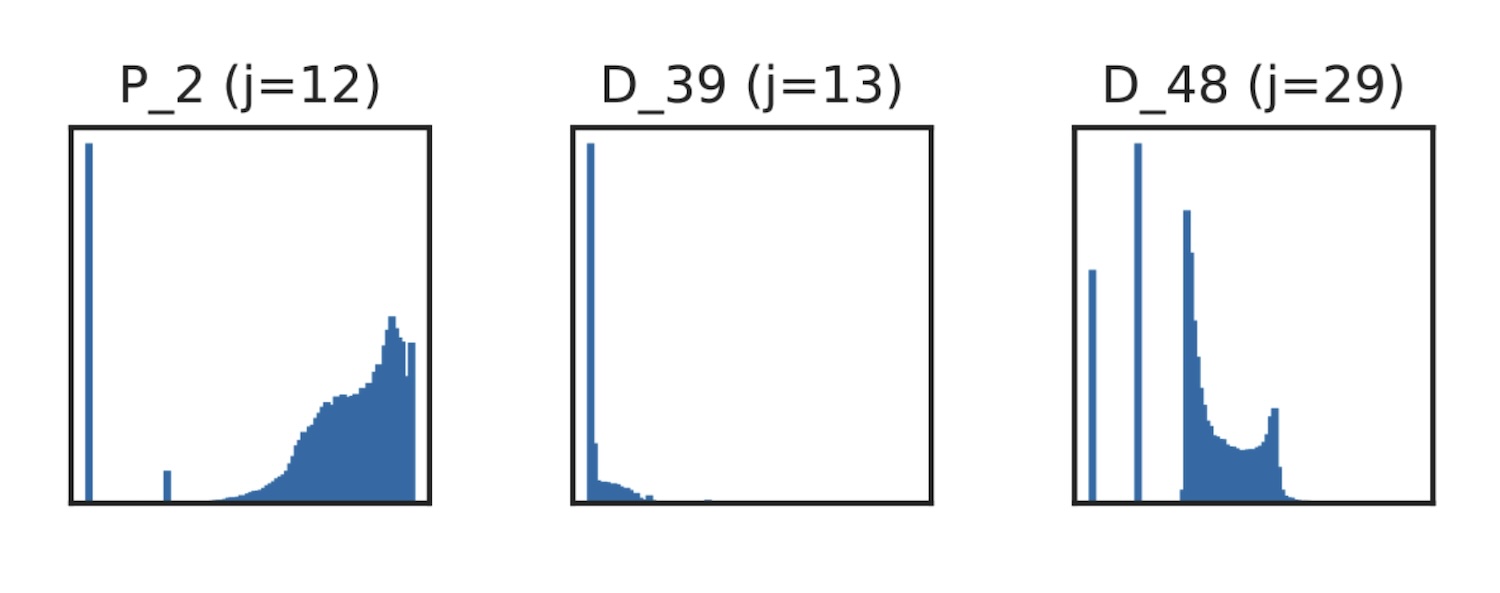
Figure 1: Histogram of three different variables from the American Express credit risk dataset, showing how financial data exhibit skewness, outliers, and multiple modes. “Extended Deep Adaptive Input Normalization for Preprocessing Time Series Data for Neural Networks” by Marcus A. K. September, Francesco Sanna Passino, Leonie Goldmann, and Anton Hinel is licensed under CC BY 4.0.

Why preprocessing is essential

If these data irregularities are not appropriately treated, the model performance can degrade significantly and predictions on out of time samples might be heavily biased, especially if using a neural network model. Additionally, appropriate data preprocessing can increase model training efficiency, enabling quicker model iteration. The input will be on the same scale as the initial model weights, meaning the first couple of weight updates do not need to adjust for differences in magnitude.

Traditional preprocessing methods, like standard scaling and min-max scaling:

• Do not adequately handle common irregularities like skewness and outliers;
• Need frequent adjustments as data patterns change due to changing macroeconomic conditions;
• Often struggle with complex non-stationary financial time series.

EDAIN: A Novel Solution

Our technique introduces four key innovations:

• Automatically identifies the optimal data processing procedure for the data and problem at hand in an end-to-end fashion;
• Dynamically adjusts to changes in data distribution in non-stationary time series;
• Intelligently handles data with outliers and skewed distributions;
• Offers flexibility to work with both global and local data patterns.

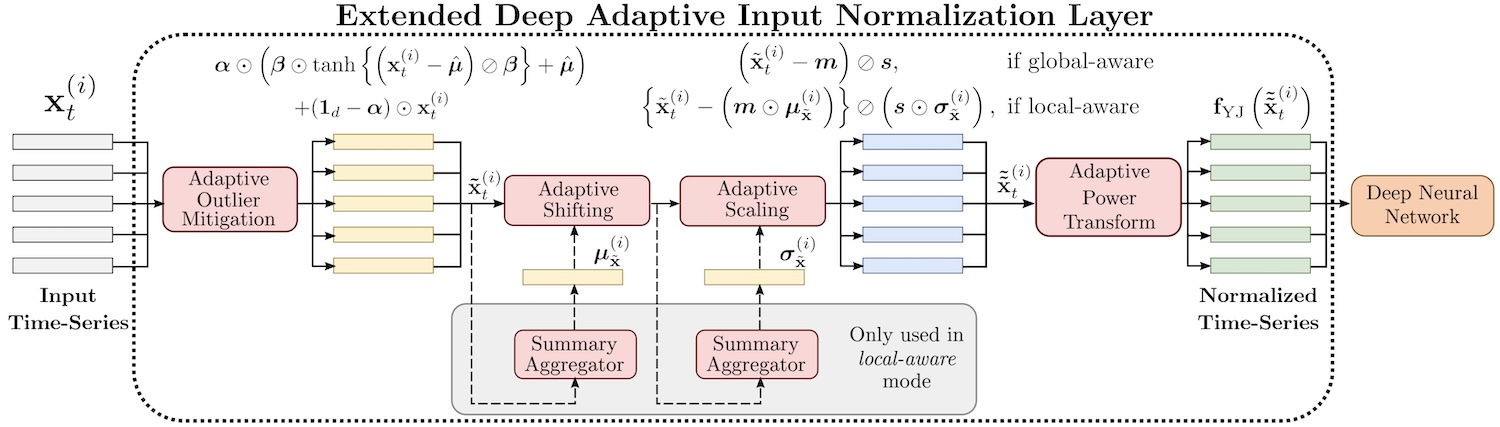
Figure 2: Architecture of the proposed EDAIN (Extended Deep Adaptive Input Normalization) layer. The input time-series is passed through four consecutive preprocessing sublayers before being fed as input to the deep neural network model. “Extended Deep Adaptive Input Normalization for Preprocessing Time Series Data for Neural Networks” by Marcus A. K. September, Francesco Sanna Passino, Leonie Goldmann, and Anton Hinel is licensed under CC BY 4.0.

How it works:

• The EDAIN method consists of four distinct sublayers applied in consecutive order.
• The first sublayer mitigates the effect of outliers with a smoothed winsorization operation using the tanh function. This results in pushing outliers closer to the regular values.
• The second and third sublayers apply a shift and scale operation, respectively, and give a similar effect as standard scaling. However, when the EDAIN layer is configured to adapt to local data patterns, the location and scale used for normalization dynamically adapts to the data.
• The fourth sublayer handles skewness by applying a Yeo-Johnson power transformation
• All the preprocessing parameters for each of the four sublayers are optimized end-to-end with the neural network model during training through stochastic gradient descent. This allows the data preprocessing to be tailored to the specific machine learning problem we are trying to solve.

We found that the method:

• Reduces manual preprocessing effort
• Improves model performance and training efficiency
• Adapts automatically to new data patterns
• Integrates seamlessly with existing neural network architectures

We compared the proposed EDAIN method against both conventional normalization methods and methods from recent research in extensive cross-validation experiments on two real-world datasets and one synthetic dataset. We found EDAIN to significantly improve accuracy across all datasets considered. These benefits can allow financial services institutions to spend less time on preprocessing their complex data and more time on improving their machine learning models elsewhere, for example, with feature engineering.

The results were promising and looking ahead, we’re looking at improving the handling of missing data, expanding applications within risk assessment, and integrating EDAIN with other machine learning innovations. If you’re interested in reading more about the process, you can read the full paper.