A Quantum Introduction for Non-Quantum Experts

Introduction

I have been intrigued by quantum physics for a very long time – even prior to taking my first quantum class as an undergraduate physics student. Over the past decade, I’ve had the opportunity to work on a wide range of quantum-related research projects involving particle accelerators, correlations between individual photons, quantum-based communication systems, and quantum algorithms. To say that I find quantum interesting would certainly be an understatement, and I’m thrilled about the potential impact that quantum technologies can have across a wide range of fields and industries.

One of the things I am most excited about related to quantum research is the increased level of interest from individuals with backgrounds and specializations outside of quantum. I believe that to fully realize the potential of quantum in the commercial space, it is imperative that quantum researchers have the ability to effectively collaborate with individuals spanning a broad spectrum of expertise. This includes customers, non-quantum researchers, engineers of varying disciplines, project managers, executive leadership, and more. Given that quantum is a relatively new area within most industries, I feel that one of my key responsibilities as a quantum researcher is education. Specifically, to help my non-quantum colleagues understand the aspects of quantum that have the potential to help them develop novel solutions for their problems of interest.

While there is a wealth of information available online related to quantum, it can be challenging to find one, concise source to serve as a well-rounded introduction to the subject for someone with a professional or personal interest.

To help rectify that, I’ve put together this brief overview to provide some foundational knowledge about quantum to help demystify it and aid in future learning. To do that, I’ll first address what quantum physics is and then provide some insight into some of the fundamental concepts that make quantum so unique, interesting, and useful from a technological standpoint.

What is Quantum Mechanics?

Quantum mechanics is a branch of physics that describes how things work at the atomic and subatomic scale. In other words, the components of the universe that are very small. It provides the most accurate description for the nature of things like atoms, protons, electrons, photons, etc. We refer to things described using quantum mechanics as quantum systems, and the way that we describe and quantify those quantum systems is through what we call quantum states. Quantum states, along with quantum superposition and non-deterministic measurement form some of the core concepts that need to be understood in order to study quantum physics. So, let’s discuss each of them in more detail using a coin flip analogy.

Quantum States

A flipped coin is certainly not a quantum system, but let’s imagine for a moment that it is. When we flip a fair coin, we know that the result will be either heads or tails. So, we can say that our coin has two possible states at the end of the flip; heads, which we will denote as H, and tails, which we will denote as T. Mathematically, we can represent these states using vectors of two-elements since there are only two possible states. If you’re not familiar with vectors, it is sufficient to think of them as bookkeeping devices for our current purposes. Using vectors, we can express our coin flip states as follows:

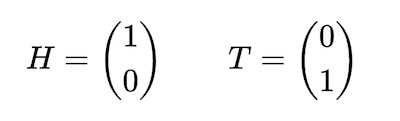
Quantum researchers often use a notation called Dirac notation, which is named after the physicist Paul Dirac, and it often makes performing certain quantum calculations less cumbersome. Since Dirac notation is so commonly used, it is worth taking one more step and expressing our quantum system and states using it. Rewriting our flipped coin quantum states in Dirac notation gives us the following:

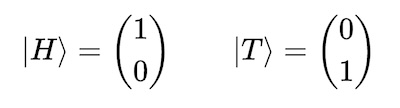
The new |···〉 symbol is called a ket. Let’s go ahead and choose to represent the general state of our quantum coin in Dirac notation as |ψ〉. We could have used any symbol inside of the ket, but I chose the psi symbol (ψ) simply because it is a common choice. With our notation sorted out, we can now formally write the result of our quantum coin flip. At the end of our coin flip, we will find that our quantum system (coin) is in one of our two possible states.

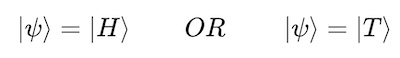
Quantum Superposition

Keeping with our quantum coin analogy, we’ve discussed what happens when we measure the coin flip, which yields one of two possible states (H or T), but what happens before that? What does the quantum state of the flipped coin look like before we measure the result? Quantum systems have a unique property called quantum superposition, which means that a quantum system can exist in multiple states at the same time. It is only through the act of measurement, or more precisely interference, that a quantum system ends up in one specific state. So, applying this to our quantum coin flip means that the coin is in both the H and T states at the same time until we measure it. This means that, formally, our quantum coin state before measurement is written as follows:

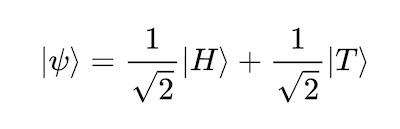
What the equation above tells us, in Dirac notation, is that our quantum coin is in both the |H〉 state (heads) and the |T〉 state (tails) at the same time before being measured. The numbers in front of the |H〉 and |T〉 states in the equation are what we call quantum amplitudes. For those of you familiar with linear algebra, these are the coefficients of a linear combination of the states. The meaning of these quantum amplitudes brings us to our final foundational concept, which is non-deterministic measurements.

Non-Deterministic Measurements

If our flipped coin was a regular, non-quantum coin, then it seems very reasonable to assume that we could create and build a device that would allow us to flip the coin in such a way that we got the same result every time. We could use something like a mechanized flipping device and shock-absorbing floor to ensure that our coin lands in the exact same way every time. In physics, we call this a deterministic system, which means if we know all of the appropriate variables well enough, we can perfectly predict the outcome of an event. If we use our highly-engineered coin flipping device and flip our non-quantum coin 1000 times, then we will record the same result 1000 times (let’s just say heads in this case).

What happens if we use our quantum coin in our coin flipping machine instead? If you conduct the same 1000 flip experiment and record the results, you will find something very odd. You will find that your coin flip resulted in heads around 50% of the time and tails the other 50% of the time. The reason for this is that quantum system measurements are probabilistic. What this means is that each possible measurement outcome of a quantum system has a probability associated with it. The theoretical probability associated with measuring a particular state can be determined using the quantum amplitudes present in our superposition equation. By applying something called the Born rule to our quantum coin example, the probabilities of measuring a heads or tails state are (PH and PT) found by squaring the magnitude of our quantum amplitudes as shown below.

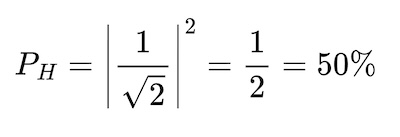
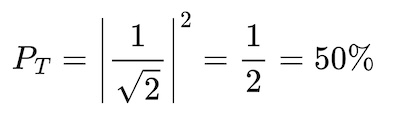
Implications of Quantum Technology

Advancements in quantum technology have the potential to cause major disruptions across a range of industries and disciplines. For example, quantum computers enable new types of algorithms with the potential to solve problems that modern computers cannot solve. However, they also create new challenges related to foundational elements of modern computing, such as security and privacy. For instance, quantum computers have the potential to break current encryption methods, jeopardizing modern security systems. This makes it imperative to develop new cryptographic techniques to ensure robust data protection. New cryptographic techniques could take the form of quantum algorithms, quantum-based physical layer protections in a communications network, or altering current algorithms to quantum-resistant versions.

The potential impact of quantum technologies is enormous, and as the technology advances, the knowledge of how to incorporate it into engineering problems will be invaluable. As a result, it will be essential that engineers and business leaders understand the impact, challenges, and opportunities that quantum research creates.